Analizzatore di spettro: come funziona?
L'analisi di spettro senza formuloni!

Audio, radiofrequenza, microonde o banda ottica: i principi di funzionamento di un analizzatore di spettro (o Spectrum Analyzer) sono simili e abbastanza semplici da comprendere, soprattutto se si evita di utilizzare formuloni, cosa che cercherò di fare in questo articolo, sperando nel perdono dei più esperti per le semplificazioni estreme che dovrò adottare.
In questo articolo:
Ann.
Ring Intercom di Amazon | Rendi smart il tuo citofono, apertura a distanza, compatibile con Alexa, audio bidirezionale (verificare la compatibilità)
- Rendi smart il tuo citofono (audio o video): puoi parlare con i visitatori e aprire il portone dell'edificio con l'app Ring. (funziona solo con i citofoni compatibili)
- Ricevi avvisi in tempo reale ogni volta che un visitatore suona al citofono e apri l'ingresso dell'edificio, direttamente dall'app Ring. La funzione di apertura a distanza ti consente di aprire il portone senza interrompere una riunione importante, sia che lavori a casa o in ufficio.
- Ring Intercom è compatibile con Alexa, quindi puoi parlare con chi suona al citofono e aprire il portone utilizzando i comandi vocali.
- Fai entrare amici e parenti in casa a orari prestabiliti: invia loro una Chiave ospite con la funzione di Verifica automatica degli ospiti.
- Progettato per l'installazione fai-da-te, Ring Intercom si collega al citofono esistente. Non comporta nessuna modifica funzionale al sistema citofonico del condominio.
- Che si tratti dei tuoi bambini, amici, familiari o di un fattorino Amazon, puoi utilizzare la

Cos'è la frequenza
Qualora non lo sapessi già, la frequenza, che si misura in Hertz (Hz) o in multipli (KHz, MHz, GHz, THz...), è il numero di ripetizioni di un fenomeno oscillatorio periodico in un secondo, cioè è l'inverso della durata (periodo = t) dell'oscillazione (1/t).
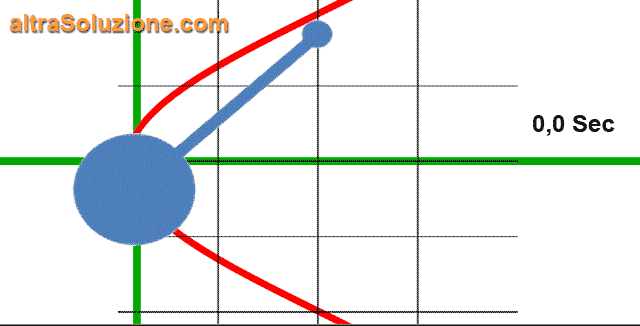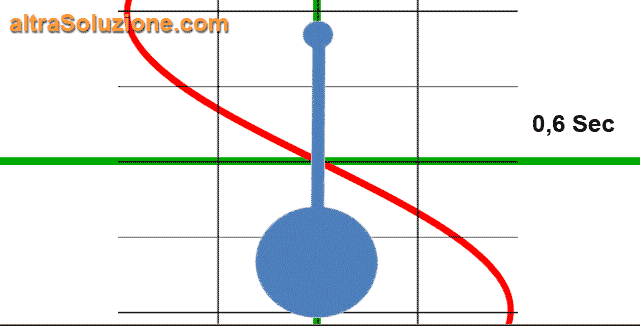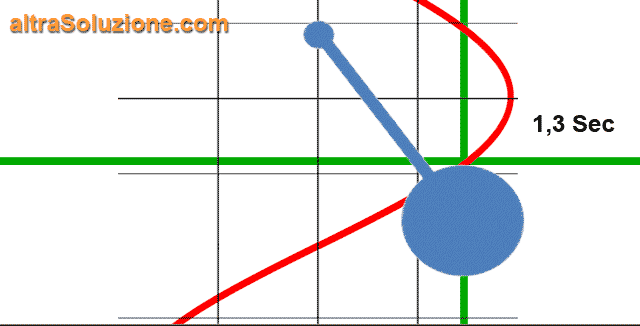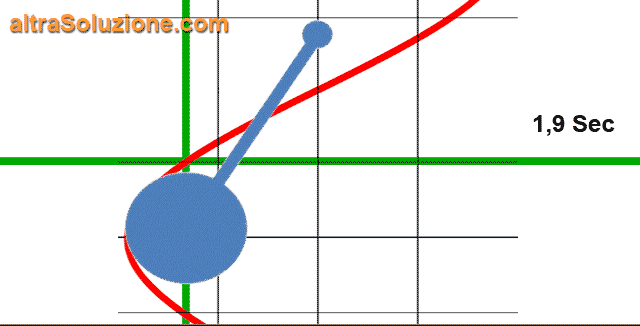
Per esempio, in un tipico orologio a pendolo, il peso oscillante compirà un ciclo completo una volta ogni
Questo significa che il pendolo oscilla a una frequenza di
Le onde sonore, le onde radio, le radiazioni elettromagnetiche e la luce sono tutti fenomeni generati dall'
Onde sonore (20 Hz - 20.000 Hz) sono emesse quando oscilla la corda di una chitarra o di un altro strumento, onde radio (30 KHz - 3 GHz) e microonde (3 GHz – 300 GHz) sono generate grazie all'oscillazione elettromagnetica di un circuito elettronico e la luce visibile (428 THz – 749 THz) non è altro che un'oscillazione elettromagnetica ad altissima frequenza emessa da corpi luminosi.
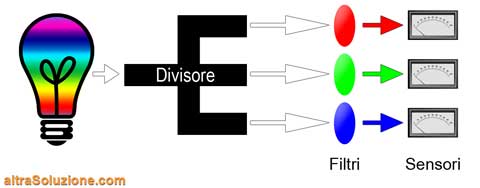
Principi di funzionamento di un analizzatore di spettro
Un analizzatore di spettro è un apparato in grado di misurare l'ampiezza (intensità) delle singole frequenze o bande (intervalli di frequenza) di un segnale complesso (somma di segnali a diverse frequenze).
Per spiegare questo concetto utilizzeremo la luce visibile e i colori.

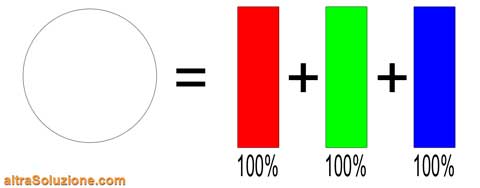
Sappiamo che la luce
Questi colori vanno dal
Se volessimo misurare l'intensità dei singoli colori (frequenze) presenti in una radiazione luminosa, dovremmo anzitutto renderli "
Quindi, per semplicità, utilizzeremo soltanto tre bande, quelle relative ai cosiddetti colori primari additivi:
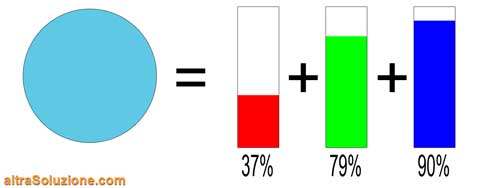
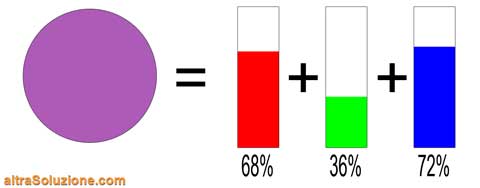
A questo punto dovremo adottare delle tecniche che separino le frequenze che compongono il colore da analizzare come, per esempio, dei filtri, dei quali poi misureremo i livelli di luce in uscita con dei sensori:
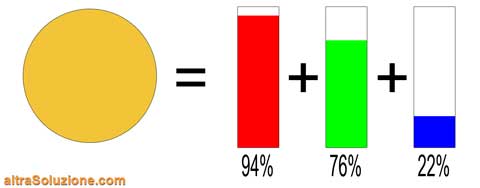
In questo modo siamo in grado di misurare separatamente i livelli delle tre componenti
Lo stesso principio è applicabile anche ad altri tipi di segnali come, per esempio, l'audio.
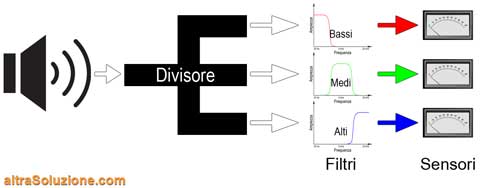
Riprendendo l'esempio precedente e considerando soltanto tre bande di frequenze (bassi, medi e alti), un analizzatore di spettro audio funziona in modo del tutto analogo, con altre tecnologie per il divisore, i filtri e i sensori:
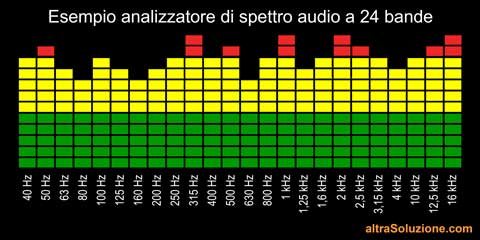
I tipici analizzatori di spettro audio, infatti, prendono il segnale d'ingresso, lo dividono tra diversi filtri, uno per banda e misurano l'uscita di ogni filtro tramite un VU-meter:
Altri metodi di misura
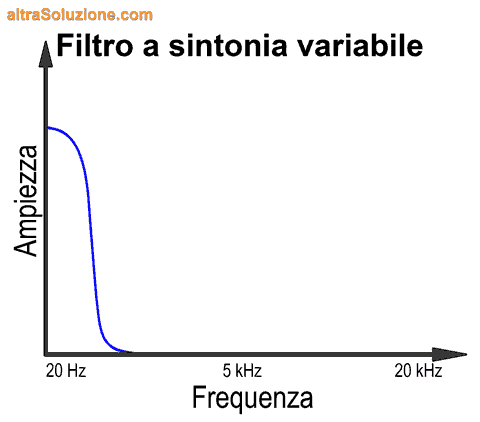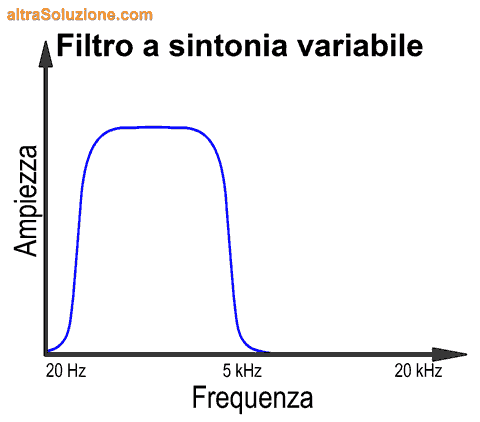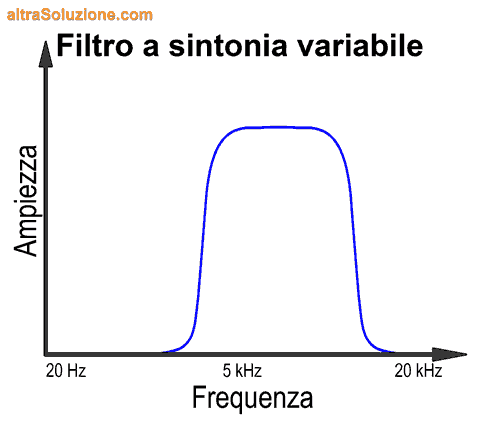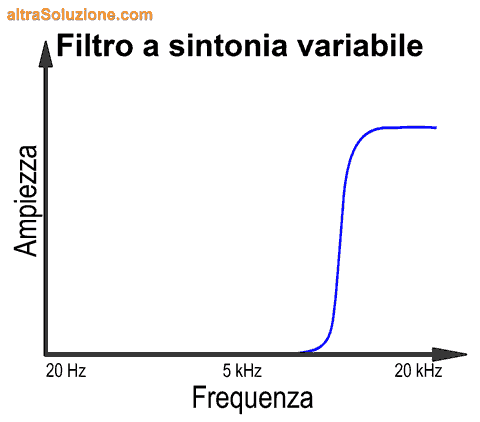
Il filtro a sintonia variabile
Il metodo appena visto dei filtri "fissi" non è sempre applicabile, sia per limiti tecnologici che per limiti economici (i filtri sono molto costosi).
Nei casi in cui non sia necessaria una visualizzazione simultanea e in tempo reale dei livelli tutte le frequenze, per esempio quando si analizza un segnale più o meno stabile nel tempo, è possibile utilizzare un metodo a "spazzata" (sweep).
In pratica, viene utilizzato un solo filtro a sintonia variabile che permette di misurare l'ampiezza delle frequenze tramite un unico sensore, al quale viene inviata una sola banda di frequenze alla volta e della quale viene memorizzata l'ampiezza, fino a comporre la curva dello spettro completa.
Ovviamente è necessario del tempo per misurare tutte le frequenze sotto analisi, quindi le misure che memorizzeremo non saranno misurate tutte nello stesso istante come, invece, avviene negli analizzatori di spettro audio di cui abbiamo parlato... e questa è la principale limitazione di questo metodo.
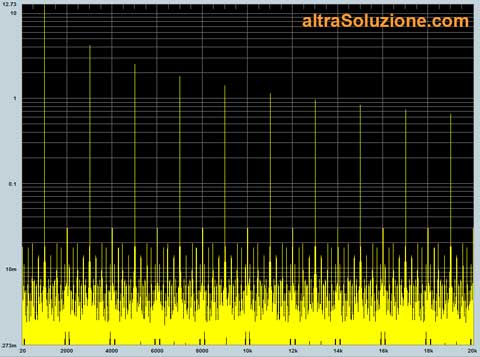
Lo so, detta così è un po' complicata, ma cercherò di spiegarmi meglio con quest'animazione:
Durante la spazzata, le misure per ogni frequenza sono memorizzate e poi presentate su uno schermo, in una visualizzazione simile a questa, nella quale vediamo lo spettro di un'onda quadra a 1 kHz con le sue armoniche:
Il tempo di spazzata (sweep time) dipende da moltissimi fattori tecnici che non sto a elencarti. Quello che devi sapere è che, se la spazzata richiede 3 secondi allora, ovviamente, al massimo riusciremo ad avere un aggiornamento delle misure ogni 3 secondi.
Come dicevo, questo può non essere un problema per analizzare un segnale costante o con variazioni molto lente ma non è utilizzabile, per esempio, in uno studio di registrazione in cui tutte le frequenze devono essere monitorate in ogni istante per verificare che non ci siano "picchi" anomali.
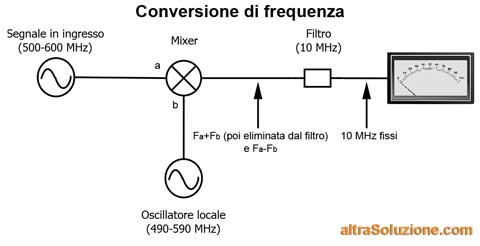
Il metodo della "conversione di frequenza"
Purtroppo, anche i filtri a sintonia variabile sono molto costosi, soprattutto quando si parla di filtri che lavorano ad alte frequenze (radiofrequenze, microonde, bande ottiche).
In questi casi, soprattutto negli analizzatori di spettro ad alta frequenza si preferisce adottare un altro metodo che è quello della conversione di frequenza, utilizzato anche nei ricevitori supereterodina, cioè praticamente in tutti gli apparecchi Radio e TV in circolazione.
Non scenderò nei dettagli tecnici perché non è lo scopo di questo articolo ma questo metodo prevede l'utilizzo di un
Quindi, inviando in un mixer due frequenze di 490 e 500 MHz, otterremo in uscita altre due frequenze di
Sfruttando questo principio e utilizzando un
Per esempio, se vogliamo analizzare frequenze
| Freq. Oscillatore Locale (MHz) | Freq. sotto analisi (MHz) | Uscita mixer (MHz) |
|---|---|---|
| 490 | 500 | 10 |
| 500 | 510 | 10 |
| 510 | 520 | 10 |
| 520 | 530 | 10 |
| 530 | 540 | 10 |
| 540 | 550 | 10 |
| 550 | 560 | 10 |
| 560 | 570 | 10 |
| 570 | 580 | 10 |
| 580 | 590 | 10 |
| 590 | 600 | 10 |
Anche in questo caso, il tempo necessario per misurare tutta la banda è variabile e dipendente da diversi fattori quindi, anche in questo tipo di misura, non è possibile analizzare le diverse frequenze in tempo reale e simultaneamente.
La trasformata di Fourier
Oggigiorno, grazie alla velocità sempre più alta e al costo sempre più basso dei
In breve, questo metodo si basa sul campionamento del segnale da analizzare (cioè della sua conversione da analogico a digitale) e sull'applicazione di un metodo matematico per calcolare le frequenze e le relative ampiezze delle componenti del segnale sotto analisi.
I moderni microprocessori sono in grado di fare questi calcoli molto velocemente, tanto da fornirci i risultati
Per maggiori informazioni su questo metodo puoi consultare Wikipedia.
Se vuoi chiedere ulteriori spiegazioni o se vuoi esprimere la tua opinione non esitare a
Ti ricordo anche che le  cambiano ogni giorno ed è il marketplace che offre le
cambiano ogni giorno ed è il marketplace che offre le
Grazie per avermi letto fin qui!